Geovana França
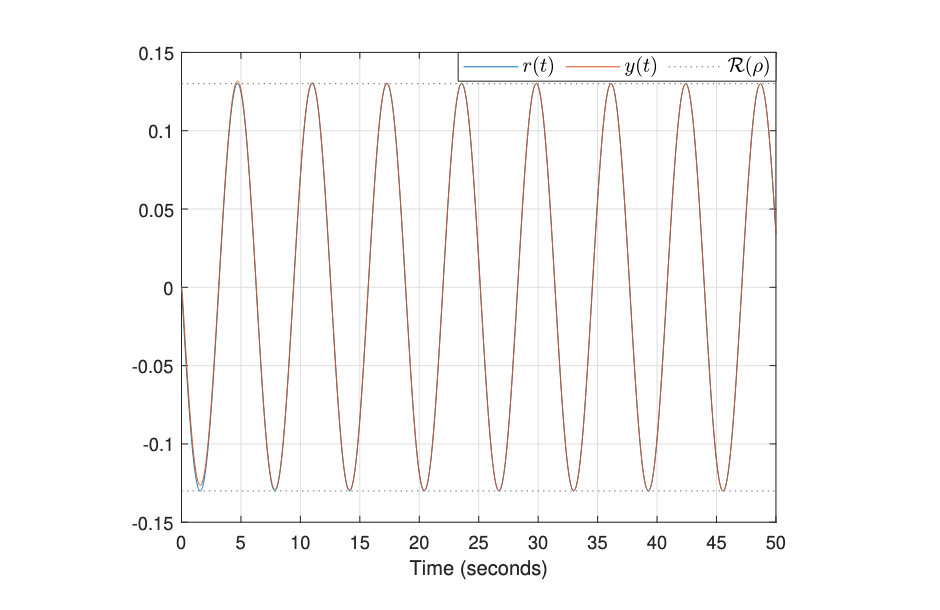
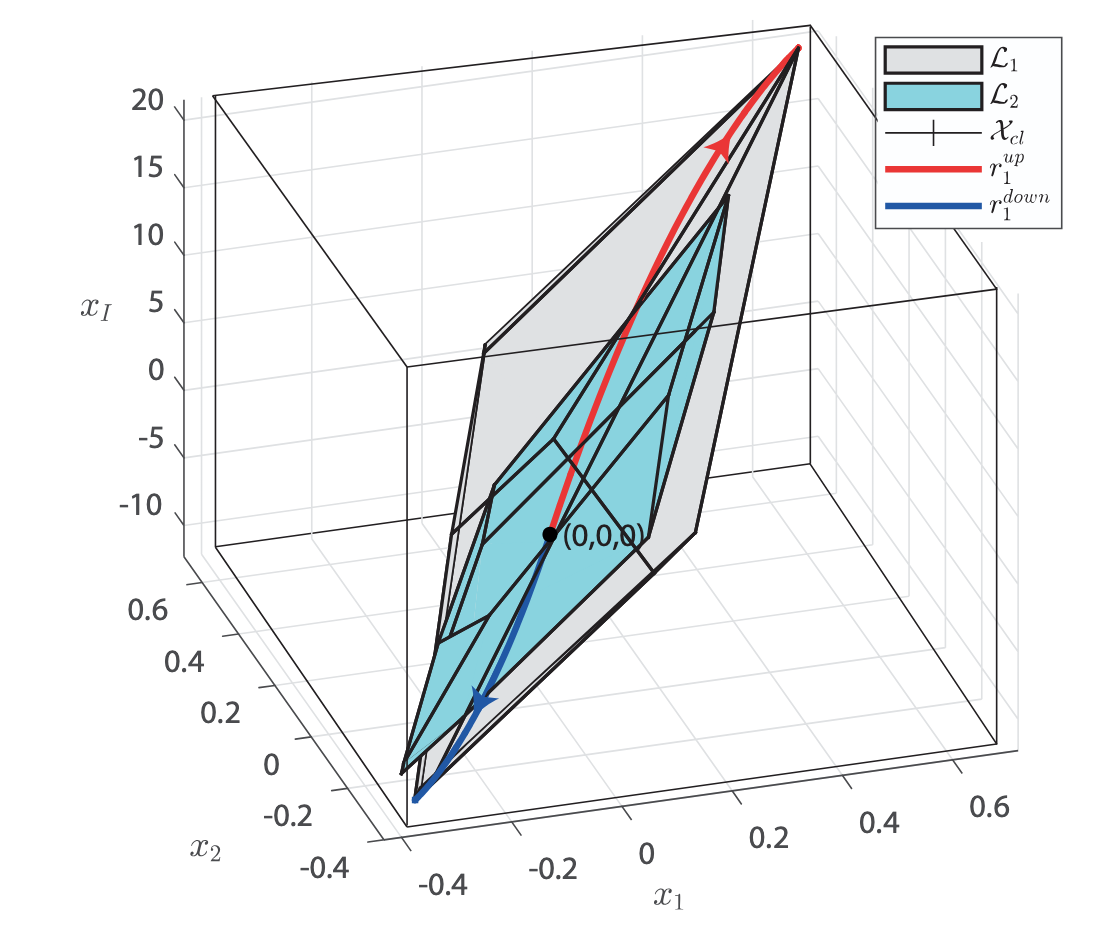
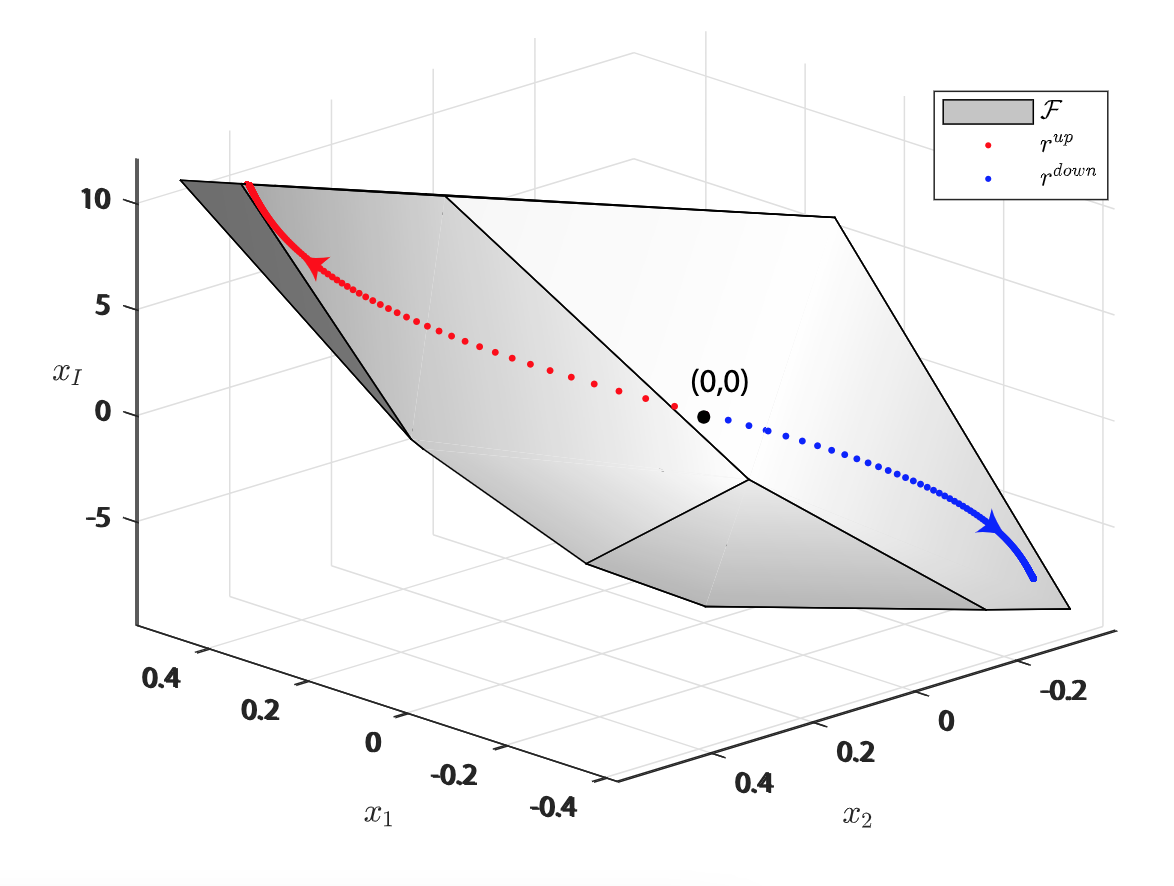
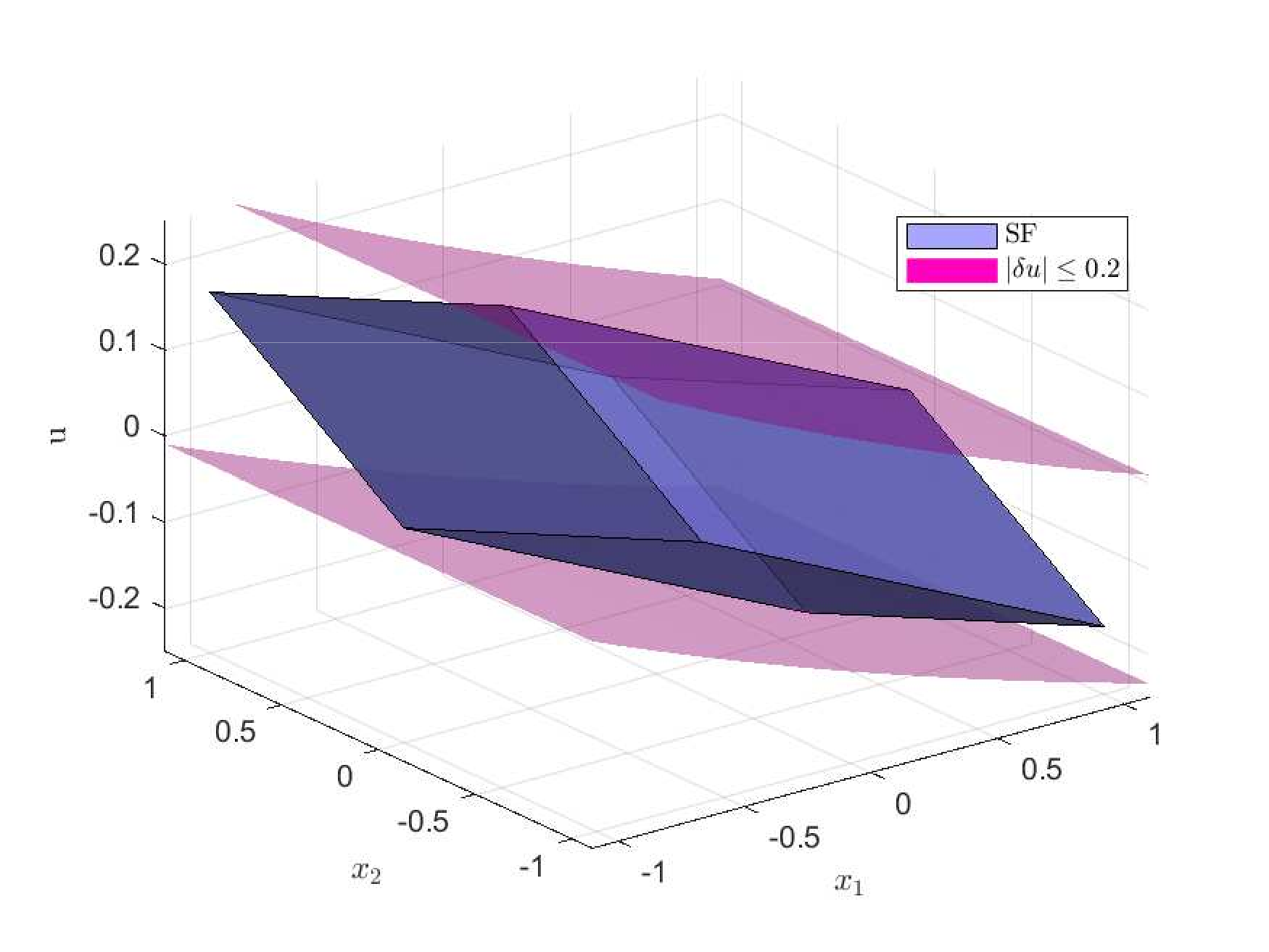
Ph.D. candidate in Information and Systems Engineering, pursuing a cotutelle between Concordia University, Canada, and the Federal University of Santa Catarina, Brazil. My research focuses on developing optimal controllers for autonomous systems that must follow precise trajectories while respecting constraints, like physical boundaries, speed limits, and disturbances.
As a mathematician with 5+ years of teaching experience, I'm passionate about bridging abstract theory and practical applications. I'm particularly drawn to emerging fields where math plays a central role—from AI and machine learning to robotics and autonomous systems.
Research Interests
Constrained Control
- Output Feedback PID Controllers
- Robust Positive Invariant
- Linear Matrix Inequalities
Applied Math
- Optimization & Operations Research
- Machine Learning
- Data Analysis